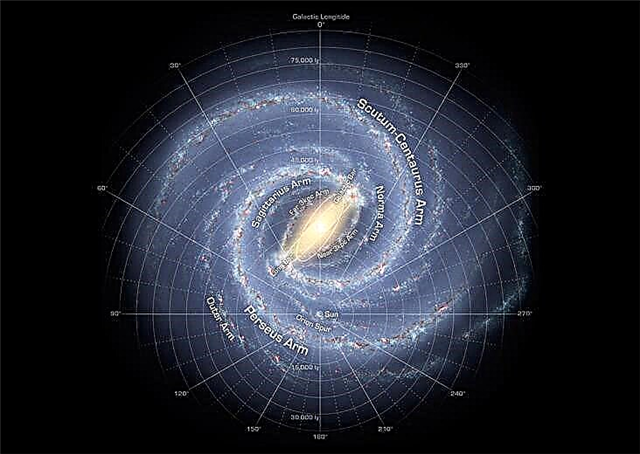
Создание летательного аппарата для Марса имело бы значительные преимущества для исследования поверхности. Это всего лишь 1,6% от плотности земного воздуха на уровне моря, дать или взять. Это означает, что обычные самолеты должны были бы летать на Марсе очень быстро, чтобы оставаться в воздухе. Ваша средняя Сессна будет в беде.
Но природа может предоставить альтернативный взгляд на эту проблему.
Текучий режим любого летающего (или плавающего) животного, машины и т. Д. Можно суммировать с помощью так называемого числа Рейнольдса (Re). Re равно характеристической длине х скорости х плотности жидкости, деленной на динамическую вязкость. Это мера отношения сил инерции к силам вязкости. Ваш средний самолет летит с высокой Re: много инерции относительно воздушной липкости. Поскольку плотность воздуха на Марсе низкая, единственный способ получить эту инерцию - это двигаться очень быстро. Однако не все летчики работают с высоким Re: большинство летающих животных летают с гораздо более низким Re. В частности, насекомые действуют при достаточно малых числах Рейнольдса (условно говоря). На самом деле, некоторые насекомые настолько малы, что плавают в воздухе, а не летают. Таким образом, если мы немного увеличим размер жука, похожего на жука, или маленькую птичку, мы можем получить что-то, что может двигаться в атмосфере Марса, не двигаясь безумно быстро.
Нам нужна система уравнений, чтобы ограничить нашего маленького бота. Оказывается, это не так уж сложно. В качестве грубого приближения мы можем использовать уравнение средней частоты колебаний Колина Пенникуика. Исходя из ожиданий частоты взмахов от Pennycuick (2008), частота взмахов колеблется примерно как масса тела до 3/8, гравитационное ускорение до 1/2, охват до -23/24, площадь крыла до -1 / 3 мощности и плотности жидкости до -3/8 мощности. Это удобно, потому что мы можем приспособиться к марсианской гравитации и плотности воздуха. Но нам нужно знать, разумно ли мы сбрасываем вихри с крыльев. К счастью, есть и известная связь: число Струхаля. Str (в данном случае) - амплитуда взлета и частота взмаха, деленная на скорость. В крейсерском полете это оказывается довольно стесненным.
Следовательно, наш бот должен иметь Str от 0,2 до 0,4, в то время как он соответствует уравнению Пенникуика. И, наконец, нам нужно получить число Рейнольдса в диапазоне для большого живого летающего насекомого (крошечные насекомые летают в странном режиме, когда большая часть движущей силы основана на сопротивлении, поэтому мы пока их игнорируем). Hawkmoths хорошо изучены, поэтому у нас есть их диапазон Re для различных скоростей. В зависимости от скорости она колеблется от 3500 до 15000. Так что где-нибудь на этом стадионе будет делать.
Есть несколько способов решения системы. Элегантный способ состоит в том, чтобы генерировать кривые и искать точки пересечения, но быстрый и простой способ - вставить его в матричную программу и решить итеративно. Я не буду предлагать все возможные варианты, но вот тот, который сработал, чтобы дать идею:
Масса: 500 грамм
Пролет: 1 метр
Соотношение сторон крыла: 8.0
Это дает Str 0,31 (прямо на деньги) и Re 13,900 (прилично) при коэффициенте подъема 0,5 (что является разумным для крейсерской). Чтобы дать представление, у этого бота были бы примерно птичьи пропорции (похожие на утку), хотя и немного с легкой стороны (не жесткие с хорошими синтетическими материалами). Однако он будет проходить через большую дугу с более высокой частотой, чем птица здесь на Земле, поэтому он будет выглядеть как гигантский мотылек на расстоянии от наших обученных Земле глаз. В качестве дополнительного бонуса, поскольку этот бот летит в режиме мотылька Рейнольдса, вполне вероятно, что он сможет прыгать к очень высоким коэффициентам подъема насекомых в течение коротких периодов, используя неустойчивую динамику. При CL 4,0 (который был измерен для маленьких летучих мышей и мухоловок, а также некоторых крупных пчел) скорость сваливания составляет всего 19,24 м / с. Макс CL наиболее полезен для посадки и запуска. Итак: можем ли мы запустить наш бот со скоростью 19,24 м / с?
Для забавы, давайте предположим, что наш птичий бот-бот также запускается как животное. Животные не взлетают как самолеты; они используют баллистическое инициирование, отталкивая от основания. Теперь насекомые и птицы используют для этого ходячие конечности, а летучие мыши (и, вероятно, птерозавры) используют крылья для удвоения в качестве толкающих систем. Если мы сделали наши крылья ботов толкающими, то мы можем использовать тот же мотор для запуска, что и для полета, и получается, что толчка не требуется. Благодаря низкой гравитации Марса даже небольшой скачок проходит долгий путь, и крылья уже могут биться около 19,24 м / с как есть. Так что небольшой прыжок сделает это. Если мы чувствуем себя модно, мы можем нанести немного больше удара, и это получится из кратеров и т. Д. В любом случае, наш бот должен быть всего на 4% эффективнее прыжка, чем хорошие биологические прыгуны, чтобы сделать это до скорости.
Эти цифры, конечно, просто грубая иллюстрация. Есть много причин, по которым космические программы еще не запустили роботов этого типа. Проблемы с развертыванием, энергоснабжением и обслуживанием сделали бы эти системы очень сложными для эффективного использования, но это не может быть вообще невозможным. Возможно, когда-нибудь наши роверы развернут бабочек размером с утку для лучшей разведки в других мирах.