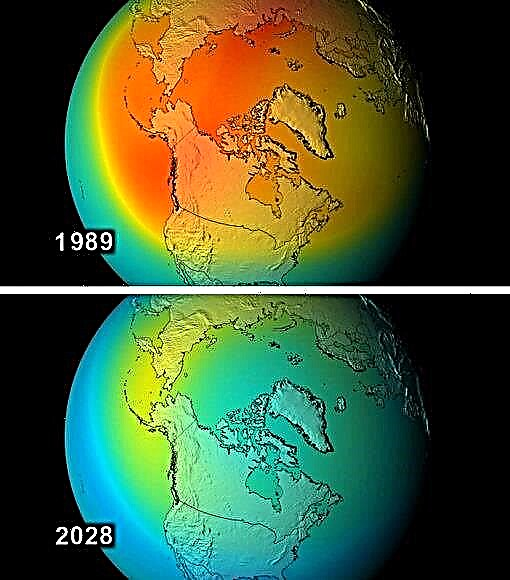
Надпись: Вид на Луну в перигее и апогее
Как учитель, я всегда в поиске лабораторий с простыми настройками, подходящими для студентов. Мой нынешний фаворит - найти скорость света с шоколадом.
В новой статье, недавно загруженной в arXiv, Кевин Кришунас из Техаса A & M описывает метод определения эксцентриситета Луны с удивительно низкой ошибкой, используя не более чем метрическую ручку, кусок картона и программу, предназначенную для подгонки кривых к переменные звезды.
Этот метод использует тот факт, что эксцентриситет может быть определен из отношения среднего углового размера объекта и половины его амплитуды. Таким образом, основной целью является измерение этих двух величин.
Стратегия Кевина заключается в том, чтобы использовать картонное смотровое отверстие, которое может скользить вдоль измерительной палки. Вглядываясь в лунное отверстие и двигая карточку взад-вперед, пока угловой размер отверстия не перекрывает луну. Оттуда диаметр отверстия, деленный на расстояние до измерительного стержня, дает угловой размер благодаря формуле малого угла (? = D / D в радианах, если D >> d).
Во избежание систематических ошибок в неправильной оценке, когда карта сдвигается вперед до тех пор, пока размер отверстия не совпадает с луной, лучше также подойти к ней с другого направления; Исходя из дальнего конца метра палки. Это должно помочь уменьшить количество ошибок, и в попытке Кевина он обнаружил, что при этом у него был типичный разброс ± 4 мм.
На этом этапе существует еще одна систематическая ошибка, которую необходимо учитывать: зрачок имеет конечный размер, сопоставимый с прицельной дырой. Это приведет к недооценке фактического углового размера. Таким образом, поправочный коэффициент необходим.
Чтобы вывести этот поправочный коэффициент, Кевин установил 91-миллиметровый диск на расстоянии 10 метров (это должно дать диск того же углового размера, что и луна, если смотреть с этого расстояния). Для изготовления наилучшего совпадения накладка из картона с прицельным отверстием должен его нужно поместить на 681,3 мм на измерительную ручку, но из-за систематической ошибки зрачка Кевин обнаружил, что его нужно поместить на 821 мм. Отношение наблюдаемого размещения к правильному размещению обеспечило поправочный коэффициент, использованный Кевином (1,205). Это необходимо будет откалибровать для каждого отдельного человека, а также будет зависеть от количества света во время наблюдения, поскольку это также влияет на диаметр зрачка. Однако принятие единого поправочного коэффициента дает удовлетворительные результаты.
Это учитывает правильно взятые данные, которые затем могут быть использованы для определения необходимых величин (средний угловой размер и 1/2 амплитуды). Чтобы определить это, Кевин использовал программу, известную как PERDET, которая предназначена для подгонки синусоидальных кривых к колебаниям переменных звезд. Любая программа, которая могла бы приспособить такие кривые к точкам данных, используя?2 подходит или анализ Фурье будет подходящим для этой цели.
Из таких программ после определения среднего углового размера и половины амплитуды их соотношение обеспечивает эксцентриситет. Для эксперимента Кевина он нашел значение 0,039 ± 0,006. Кроме того, период, который он определил от перигея до перигея, составлял 27,24 ± 0,29 дня, что отлично согласуется с принятым значением 27,55 дня.